728x90
반응형
트리
- 노드를을 간선으로 연결한 계층 형 자료구조.
- 제일 위의 하나의 노드를 루트 노드로 하여 나머지 노드들이 간선으로 연결.
- 하나의 노드는 그 자체로 트리이며 루트가 된다.
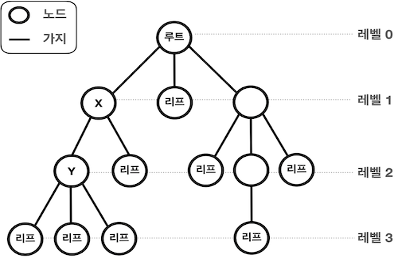
트리의 용어
| 트리 용어 | 설명 |
| 루프 | 트리의 가장 윗부분에 위치하는 노드. 하나의 트리에 하나의 루트가 존재한다. |
| 리프 | 트리의 가장 아랫부분에 위치하는 노드. 더 이상 뻗어 나갈 수 없는 노드를 일컫는다. |
| 안쪽 노드 | 루트를 포함하여 리프를 제외한 노드 |
| 부모 | 어떤 노드에서 가지로 연결된 위쪽 노드 |
| 자식 | 어떤 노드 로부터 가지로 연결된 아래쪽 노드 |
| 형제 | 같은 부모를 가지는 노드 |
| 조상 | 어떤 노드에서 가지로 연결된 위쪽 노드 모두 |
| 자손 | 어떤 노드에서 가지로 연결된 아래쪽 노드 모두 |
| 레벨 | 루트로부터 얼마나 떨어져 있는지에 대한 값을 레벨 루트의 레벨은 0 |
| 차수 | 노드가 갖는 자식의 수 |
| 높이 | 루트부터 가장 멀리 떨어진 리프까지의 거리 |
트리의 종류
| 트리 용어 | 설명 |
| 서브 트리 | 트리 안에서 다시 어떤 노드를 루트로 정하고 그 자손으로 이루어진 트리 |
| 널 트리 | 노드, 가지가 없는 트리 |
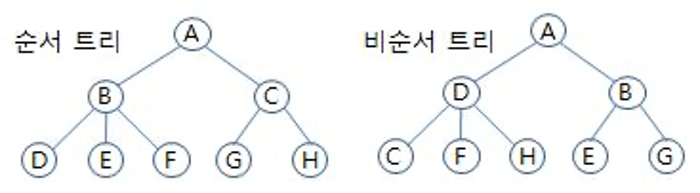
| 순서 트리 | 형제 노드의 순서를 따지는 트리 |
| 무순서 트리 | 형제 노드의 순서를 따지지 않는 트리 |
트리의 탐색
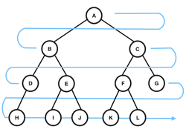
너비 우선 탐색(breadth-fisrt-search)
- 낮은 레벨에서 시작해 왼쪽 → 오른쪽 방향으로 검색한다.
- 한 레벨에서의 검색이 끝나면 다음 레벨로 내려간다.
- 검색 순서는 다음과 같다.
A -> B -> C -> D -> E -> F -> G -> H -> I -> J -> K -> L
깊이 우선 탐색(depth-first-search)
- 리프까지 내려가면서 검색하는 것을 우선순위로 하는 탐색 방법
- 리프에 도달해 더 이상 검색을 진행할 곳이 없는 경우 ,부모에게 돌아간다.
- 그 다음 다시 자식 노드로 내려간다.
 |
 |
| 너비 우선 탐색 | 깊이 우선 탐색 |
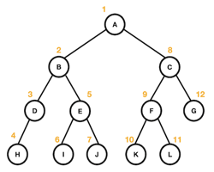
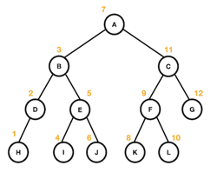
트리의 순회
| 선위 순회 | 중위 순회 | 후위 순회 |
 |
 |
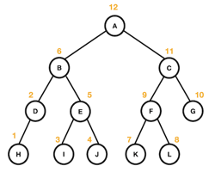 |
| 노드 방문 → 왼쪽 자식 → 오른쪽 자식 | 왼쪽 자식 → 노드 방문 → 오른쪽 자식 | 왼쪽 자식 → 오른쪽 자식 → 노드 방문 |
| A -> B -> C -> H -> E-> I -> J -> C -> F -> K -> L -> G | H -> D -> B -> I -> E -> J -> A -> K -> F -> L -> C -> G | H -> D -> I -> J -> E -> B -> K -> L -> F -> G -> C -> A |
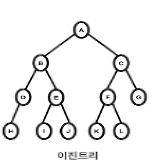
이진트리
노드가 왼쪽 자식과 오른쪽 자식을 갖는 트리를 이진 트리라고 한다.
각 노드의 자식은 2개 이하여야 한다.
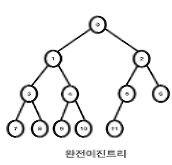
이진트리의 종류
| 완전 이진트리 | 루트부터 노드가 채워져 있으면서 같은 레벨에서 왼쪽 오른쪽 순으로 노드가 채워져 있는 트리 |
| 적정 이진트리 | 각 내부 노드가 두 개의 자식 노드를 갖는 순서화 된 트리 |
| 포화 이진트리 | 모든 리프 노드의 레벨이 동일하고 모든 레벨이 가득 채워져 있는 트리 |
 |
 |
이진검색트리(binary search tree)
이진검색트리는 이진트리가 다음 조건을 만족하면 된다.
- 어떤 노드 N을 기준으로 왼쪽 서브 트리 노드의 모든 키 값은 노드 N의 키 값보다 작아야 한다.
- 오른쪽 서브 트리 노드의 키 값은 노드 N의 키 값보다 커야 한다.
- 같은 키 값을 갖는 노드는 없다.
반응형
오일러 투어 순회
- 선위, 중위, 후위 순회를 모두 합친 형태
- 이진트리에 대한 일반순회(generic traversal)
- 각 노드를 세 번 방문하므로 위 셋 중 한가지 순회만으로 성취하기 어려운 작업 수행

728x90
반응형
'Datastructure' 카테고리의 다른 글
| [스택과 큐] #5. 덱 (0) | 2022.02.14 |
|---|---|
| [스택과 큐] #4. 큐 함수 (0) | 2022.02.14 |
| [스택과 큐] #3. 큐 (0) | 2022.02.14 |
| [스택과 큐] #2. 스택 함수 (0) | 2022.02.12 |
| [스택과 큐] #1. 스택 (0) | 2022.02.11 |



