트리 ADT
트리의 정의
• 트리는 계층적 데이터 구조로, 상위 노드에서 하위 노드로 분기되는 형태를 가진다.
• 회사 조직도를 예로 들어, 대표 아래에 제조부, 연구부 등의 부서가 있고, 그 아래에는 더욱 세부적인 부서들이 있다.
트리는 조직 구성, 파일 시스템, 프로그래밍 환경 등 다양한 데이터 모델에 직접적으로 활용될 수 있으며, 특정 알고리즘을 위한 보조 데이터 구조나 다른 복잡한 데이터 구조의 부분적 요소로 간접적으로 활용될 수 있다.
트리 용어
트리이에 대한 알고리즘을 학습하기 전, 트리와 관련된 용어들의 설명은 아래와 같다.
트리는 리스트, 스택, 큐, 집합과 같은 1차원의 선형 데이터 구조와 달리 계층구조에 의한 2차원적 구조를 가지므로 선형에 비해 한 차원 높은 정보를 다룰 수 있는 만큼 관련 용어가 많다.
1. 노드(Node)와 간선(Edge)
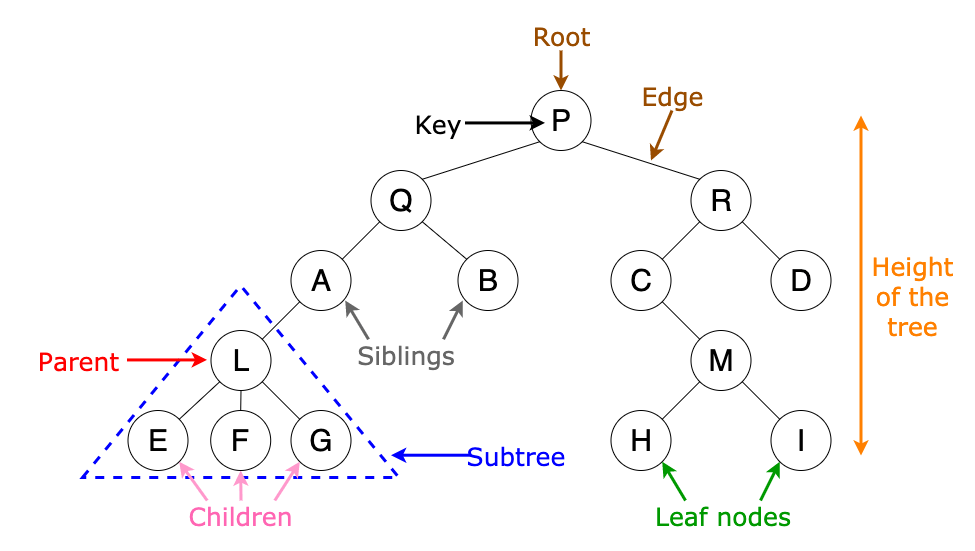
노드(node): 데이터 원소를 나타내며, 그림에서는 상자로 표현됨.
간선(edge): 노드 간의 관계를 나타내며, 그림에서는 선으로 표현됨.
트리 구조
⸰ 트리 ADT는 계층적으로 저장된 데이터 요소들을 모델링하며, 각 트리 원소는 0개 이상의 자식(children) 원소들을 가지며, 트리 계층 구조 맨 위의 원소를 제외하고는 하나의 부모(parent) 원소를 가진다.
비어 있지 않은 트리
⸰ 트리는 비어 있지 않다고 가정한다.
⸰ 이는 트리 관련 알고리즘에서 트리가 비어 있는 경우를 별도로 처리하지 않아도 되어 알고리즘 작성이 단순해지는 장점이 있다.
⸰ 만약 실제로 비어 있는 트리를 다루어야 한다면 별도의 코드를 추가해야 한다.
트리의 노드 설명은 아래와 같다.
• 루트 노드(Root Node): 트리의 최상위 노드로 부모가 없는 노드.
• 내부 노드(Internal Node): 자식이 있는 노드.
• 외부 노드(External Node) 또는 리프 노드(Leaf Node): 자식이 없는 노드.
• 형제(Sibling): 같은 부모를 가진 노드들.
• 조상(Ancestor): 루트를 향해 올라가면서 만나는 부모, 조부모 등의 상위 노드들.
• 자손(Descendant): 아래로 내려가면서 만나는 자식, 손주 등의 하위 노드들.
• 서브트리/부트리(Subtree): 특정 노드와 그 자손들로 이루어진 트리.
2. 경로(Path)
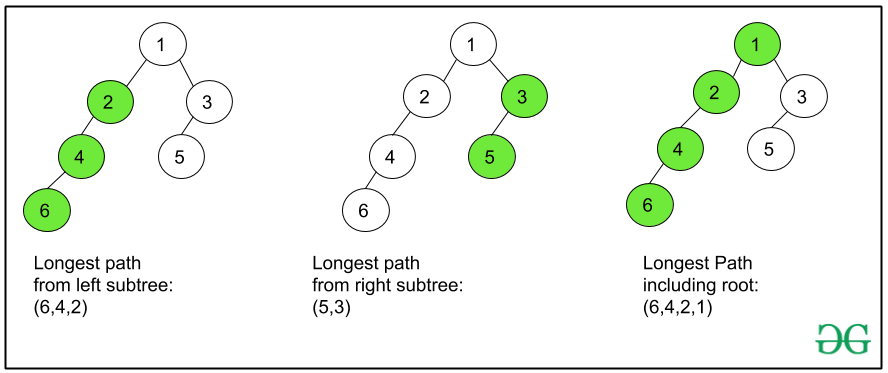
• 경로: 조상 또는 자손을 따라 이어진 노드의 시퀀스.
• 경로 길이(Path Length): 경로 내 간선의 수.
⸰ 노드의 깊이(Depth): 루트로부터 노드까지의 경로 길이.
⸰ 노드의 높이(Height): 노드로부터 리프까지의 가장 긴 경로 길이.
⸰ 트리의 높이(Height of a Tree): 루트 노드의 높이.
3. 순서트리와 무순트리
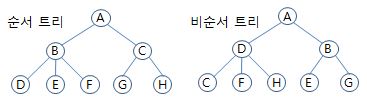
순서트리(Ordered Tree)
• 각 노드의 자식들에 대한 선형 순서가 정의된 트리.
• 예를 들어, 구조적 문서와 같이 요소들의 순서가 정해져 있는 경우.
무순트리(Unordered Tree)
• 자식 노드의 순서가 중요하지 않은 트리.
• 예를 들어, 조직 구성도에서 부서의 순서가 중요하지 않은 경우.
트리 ADT 메쏘드
| 일반 메쏘드 ▷ boolean isEmpty() ▷ integer size() 접근 메쏘드 ▷ node root() ▷ node parent(v) ▷ node children(v) ▷ element element(v) |
질의 메쏘드 ▷ boolean isInternal(v) ▷ boolean isExternal(v) ▷ boolean isRoot(v) 갱신 메쏘드 ▷ swapElements(v, w) ▷ element setElement(v, e) 예외 ▷ invalidNodeException(): 불법 노드 접근 시 발령트리 ADT를 구현하는 데이터구조에 따라 추가적인 갱신 메쏘드(삽입,삭제 등) 정의 가능 |
트리 응용
| 직접 응용 | 간접 응용 |
| 조직구성도 • 내부노드: 부, 과, 팀 등 • 외부노드: 직원 파일시스템 • 내부노드: 폴더(folders 또는 directories) • 외부노드: 파일 프로그래밍 환경 • 내부노드: 프로그램 구조물(programming constructs) • 외부노드: 어휘, 상수, 심볼 |
• 알고리즘을 위한 보조 데이터구조 • 다른 데이터구조를 구성하는 요소 |
깊이
∙ 정의: 노드 v의 깊이는 루트로부터 해당 노드까지의 경로 길이입니다.
∙ 루트 노드: 깊이는 0입니다.
∙ 비루트 노드: 깊이는 부모 노드의 깊이 + 1입니다.
∙ 재귀적 정의
1. 루트 노드: 만약 v가 루트면, v의 깊이는 0입니다.
2. 일반 노드: 그렇지 않으면, v의 깊이는 v의 부모의 깊이 + 1입니다.
∙ 실행시간 O(n)
- n은 트리 내 총 노드 수입니다.
- 각 노드의 깊이를 계산하기 위해 트리의 각 노드를 한 번씩 방문해야 하므로, 전체 실행시간은 O(n)입니다.
∙ 특징: depth(v)는 트리의 구체적인 구현 방식과 독립적입니다. 즉, 이 정의는 트리의 형태나 저장 방식에 상관없이 적용될 수 있습니다.
| Alg depth(v) if (isRoot(v)) return 0 else return 1 + depth(parent(v)) |
높이
∙ 노드 v의 높이(height)의 재귀적 정의
- 만약 v가 외부노드면, v의 높이는 0이다.
- 그렇지 않으면, v의 높이는 v의 자식들 중 최대 높이 더하기 1이다.
∙ 실행시간: O(n) – 단, n은 트리 내 총 노드 수이다.
∙ 루트가 r인 트리의 높이(height of a tree)는 height(r)을 호출하여 계산한다.
| Alg height(v) if (isExternal(v)) return 0 else h ← 0 for each w ∈ children(v) h ← max(h, height(w)) return 1 + h |
트리 순회 방법
순회(traversal)란 트리의 노드들을 체계적인 방식으로 방문하는 것을 말한다.
선위순회 (Preorder Traversal)
설명: 노드를 자손들보다 먼저 방문하는 순회 방법입니다.
순회 순서: 부모 → 왼쪽 자식 → 오른쪽 자식
실행시간: O(n) (n은 트리 내 총 노드 수)
응용: 트리 구조를 복사하거나, 각 노드에서 특정 작업을 수행할 때 유용합니다.
| 응용 | 예: 구조적 문서 |
| 1. 구조적 문서를 인쇄 2. 계층적 파일시스템의 모든 폴더들을 나열 |
적절한 들여쓰기를 사용하여 구조적 문서의 목차를 인쇄하고자 한다. 전제: 문서는 순서트리에 저장되어 있다. |
중위순회 (Inorder Traversal)
중위순회 (Inorder Traversal)
설명: 노드를 왼쪽 자식들 다음에, 오른쪽 자식들보다 앞서 방문합니다.
순회 순서: 왼쪽 자식 → 부모 → 오른쪽 자식
실행시간: O(n)
응용: 이진 탐색 트리(BST)에서 노드를 정렬된 순서로 방문할 때 유용합니다.
후위순회 (Postorder Traversal)
설명: 노드를 자손들보다 나중에 방문하는 순회 방법입니다.
순회 순서: 왼쪽 자식 → 오른쪽 자식 → 부모
실행시간: O(n)
응용: 트리의 노드를 삭제하거나, 노드들의 집합을 평가할 때 유용합니다.
| 응용 | 예: 디스크 사용량 |
| 계층적 파일시스템에서 폴더의 디스크 사용량 계산 | 폴더의 디스크 사용량을 계산하고자 한다. 다음 사용량의 재귀적 합을 구해 얻는다. - 폴더 자체의 사용량 (1KB라고 가정) - 폴더내 파일들의 사용량 - 자식 폴더들의 사용량 |
레벨순회 (Levelorder Traversal)
레벨(Level)의 정의
∙ 레벨 (Level) d: 트리에서 같은 깊이 d에 존재하는 모든 노드들의 집합을 의미합니다.
∙ 레벨 0: 루트 노드만이 존재합니다.
∙ 레벨순회: 큐를 이용하여 깊이 순서대로 트리의 노드들을 방문합니다.
깊이 d의 모든 노드들을 방문한 후, 깊이 d+1의 노드들을 방문한다.
즉, 같은 레벨의 노드들을 차례로 방문한 후, 다음 레벨의 노드들로 이동한다.
∙ 실행시간: O(n) (n은 트리 내의 총 노드 수)
∙ 응용: 트리의 계층 구조를 인쇄하거나, 최단 경로 탐색 알고리즘 등에 사용됩니다.
이진트리 ADT
∙ 이진트리: 각 노드가 최대 두 개의 자식을 가지는 트리입니다.
∙ 이진트리의 성질: 노드 수, 외부노드 수, 내부노드 수, 트리의 높이 등의 관계를 정의합니다.
추가 메소드:
▶ leftChild(v): 노드 v의 왼쪽 자식을 반환합니다.
▶ rightChild(v): 노드 v의 오른쪽 자식을 반환합니다.
▶ sibling(v): 노드 v의 형제를 반환합니다.
이진트리 순회
∙ 선위순회 (Preorder): 노드를 왼쪽 및 오른쪽 자식들보다 먼저 방문합니다.
∙ 후위순회 (Postorder): 노드를 왼쪽 및 오른쪽 자식들 다음에 방문합니다.
∙ 중위순회 (Inorder): 노드를 왼쪽 자식들 다음에, 오른쪽 자식들보다 앞서 방문합니다.
배열에 기초한 이진트리
∙배열 표현
각 노드의 위치는 순위로 정의되며, 순위 i의 노드에 대해 왼쪽 자식의 위치는 2i, 오른쪽 자식의 위치는 2i + 1, 부모의 위치는 ⌊i/2⌋입니다.
메서드:
▶ element(v): 노드 v의 요소를 반환합니다.
▶ root(): 루트 노드를 반환합니다.
▶ isRoot(v): 노드 v가 루트인지 확인합니다.
▶ parent(v): 노드 v의 부모를 반환합니다.
▶ leftChild(v): 노드 v의 왼쪽 자식을 반환합니다.
▶ rightChild(v): 노드 v의 오른쪽 자식을 반환합니다.
▶ sibling(v): 노드 v의 형제를 반환합니다.
▶ isInternal(v): 노드 v가 내부노드인지 확인합니다.
▶ isExternal(v): 노드 v가 외부노드인지 확인합니다.
▶ setElement(v, e): 노드 v의 요소를 e로 설정합니다.
▶ swapElements(v, w): 노드 v와 w의 요소를 교환합니다.
연결이진트리
연결리스트 표현: 노드가 부모, 왼쪽 자식, 오른쪽 자식에 대한 정보를 가집니다.
메서드:
▶ element(v): 노드 v의 요소를 반환합니다.
▶ root(): 루트 노드를 반환합니다.
▶ isRoot(v): 노드 v가 루트인지 확인합니다.
▶ parent(v): 노드 v의 부모를 반환합니다.
▶ leftChild(v): 노드 v의 왼쪽 자식을 반환합니다.
▶ rightChild(v): 노드 v의 오른쪽 자식을 반환합니다.
▶ sibling(v): 노드 v의 형제를 반환합니다.
▶ isInternal(v): 노드 v가 내부노드인지 확인합니다.
▶ isExternal(v): 노드 v가 외부노드인지 확인합니다.
▶ setElement(v, e): 노드 v의 요소를 e로 설정합니다.
▶ swapElements(v, w): 노드 v와 w의 요소를 교환합니다.
응용문제
∙ 계승자 문제: 선위, 중위, 후위 순회 계승자 찾기
∙ 로만노드 문제: 트리의 노드 중 왼쪽과 오른쪽 부트리의 크기 차이가 일정 범위 내에 있는 노드를 찾기
∙ 양자택일식 문답 시스템: 질문에 따라 다양한 결정을 제공하는 시스템 구축
오일러 투어 순회
오일러 투어(Euler Tour): 이진트리에 대한 일반순회(generic traversal)
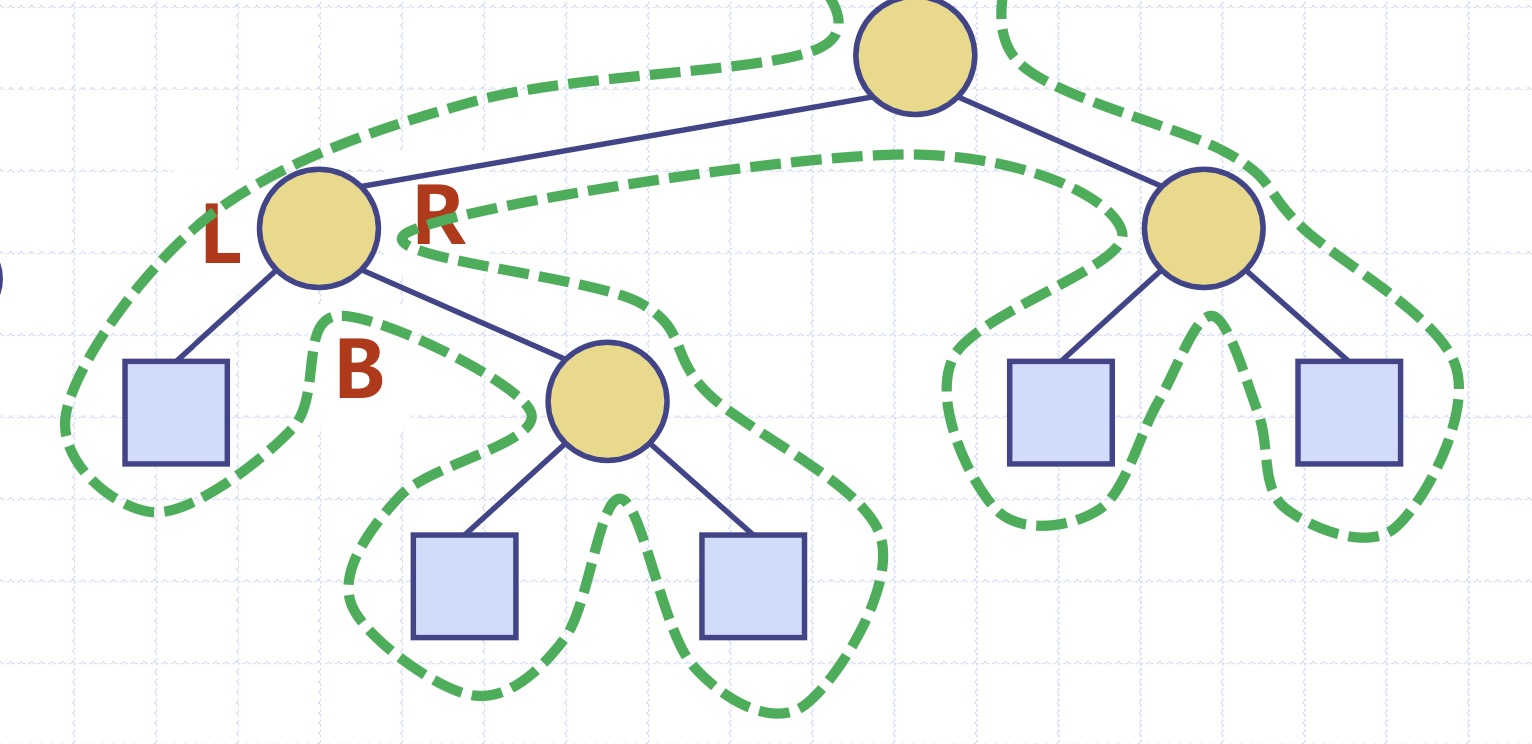
개요
오일러 투어 순회(Euler Tour Traversal)는 이진트리나 일반 트리에서 모든 노드를 세 번씩 방문하는 순회 방법입니다. 이는 트리의 모든 간선을 두 번씩 지나게 되므로, 트리의 구조를 완전히 이해할 수 있게 합니다.
정의
- 오일러 투어 순회: 트리의 각 노드를 세 번 방문하며, 각 방문은 노드의 왼쪽, 아래, 오른쪽에서 이루어집니다.
- 왼쪽 방문 (L): 노드의 왼쪽에서 방문
- 아래 방문 (B): 노드의 아래에서 방문
- 오른쪽 방문 (R): 노드의 오른쪽에서 방문
순회 방식
오일러 투어 순회는 다음과 같은 순서를 따릅니다:
- 루트 노드를 출발하여, 항상 트리의 왼쪽 벽을 따라 진행합니다.
- 각 노드를 왼쪽(L), 아래(B), 오른쪽(R) 세 번 방문합니다.
- 모든 간선을 두 번씩 지나므로, 트리의 구조를 완전히 파악할 수 있습니다.
실행시간
- O(n): 트리의 모든 노드를 세 번씩 방문하기 때문에, 실행시간은 O(n)입니다. 여기서 n은 트리 내의 총 노드 수입니다.
구현 예시
오일러 투어 순회를 구현한 알고리즘은 다음과 같습니다:
def eulerTour(node):
if node is None:
return
visitLeft(node) # Preorder
if isInternal(node):
eulerTour(leftChild(node))
visitBelow(node) # Inorder
if isInternal(node):
eulerTour(rightChild(node))
visitRight(node) # Postorder
def visitLeft(node):
# Preorder visit logic
print(f"Visiting {node} from the left")
def visitBelow(node):
# Inorder visit logic
print(f"Visiting {node} from below")
def visitRight(node):
# Postorder visit logic
print(f"Visiting {node} from the right")응용
오일러 투어 순회는 다양한 트리 알고리즘에서 유용합니다. 특히 다음과 같은 경우에 사용됩니다:
- 각 노드 방문: 선위, 중위, 후위 순회 모두 포함하여 노드를 다양한 순서로 방문해야 하는 경우.
- 부트리 크기 계산: 각 부트리의 노드 수를 계산할 때 유용합니다.
- 트리 그래프 그리기: 트리를 평면에 그릴 때 좌표를 계산하는 데 사용됩니다.
'Datastructure > [8] 트리' 카테고리의 다른 글
| [8] 트리 ⑥ 응용 (1) : 연결리스트를 이용한 트리 구현 (1) | 2024.06.05 |
|---|---|
| [8] 트리 ⑤ 스택을 이용한 이진 트리 (1) | 2024.06.04 |
| [8] 트리 ④ 레벨 순회 : 원형 큐 이용 (0) | 2024.06.03 |
| [8] 트리 ③ 원형 큐 (0) | 2024.06.03 |
| [8] 트리 ② 트리의 구현 : ADT (0) | 2024.05.30 |



