[2] 재귀

재귀

어떤 사건이 자기 자신을 포함하고 다시 자기 자신을 사용해 정의될 때 재귀적이라고 한다. 재귀를 효과적으로 사용하면 프로그램을 보다 간결하게 만들 수 있다.

 

이때 재귀에 있어 재귀는 순환 호출하는 부분과 순환을 멈추는 부분(조건문)으로 이루어져 있다. 

재귀 함수의 대표적인 장점은 아래와 같다.

 

① 알고리즘 자체가 재귀적으로 표현하기 자연스럽다. (가독성이 높아짐)

② 변수 사용을 줄여준다. (메모리 크기가 상대적으로 적어짐)

재귀 예제

순차 곱셈 구하기

코드는 아래의 [더보기] 란을 확인한다.

#include<stdio.h>
#include<string.h>
#include<stdlib.h>

int fac(int n){
    int rst;
    if(n>0) return n *fac(n-1);
    else return 1;
}

int main(){
    int n;
    printf("펙토리얼을 계산할 숫자를 입력하세요: ");scanf("%d",&n);
    printf("rst = %d",fac(n));   
}

하노이 탑 : 백준 11729

입력

첫째 줄에 첫 번째 장대에 쌓인 원판의 개수 N (1 ≤ N ≤ 20)이 주어진다.

 

3

출력

첫째 줄에 옮긴 횟수 K를 출력한다.
두 번째 줄부터 수행 과정을 출력한다. 두 번째 줄부터 K개의 줄에 걸쳐 두 정수 A B를 빈칸을 사이에 두고 출력하는데, 이는 A번째 탑의 가장 위에 있는 원판을 B번째 탑의 가장 위로 옮긴다는 뜻이다.

 

7 1 3 1 2 3 2 1 3 2 1 2 3 1 3

[ 알고리즘 분석 ]

하노이 탑의 조건은 아래와 같다.

 

① 한 번의 하나의 원판을 이동할 수 있다. 

② 맨 위에 있는 원판만 이동이 가능하다. 

③ 크기가 작은 원판 위에 크기가 큰 원판이 올라갈 수 없다. 

 

이제 하노이탑의 알고리즘을 세워보자. 먼저 n개의 원판을 가진 하노이탑 A, B, C에서 원판이 마지막 탑에 이동하는 알고리즘은 아래와 같다.

 

1. (n-1)개를 'B'로 이동 2. 남은 1개를 'C로 이동 3. (n-1)를 'C'로 이동

하노이탑의 원판이 3개로 예를 들어보자. 원판이 세 개인 경우 실제 움직인 순서는 아래와 같다.

https://mgyo.tistory.com/185

 

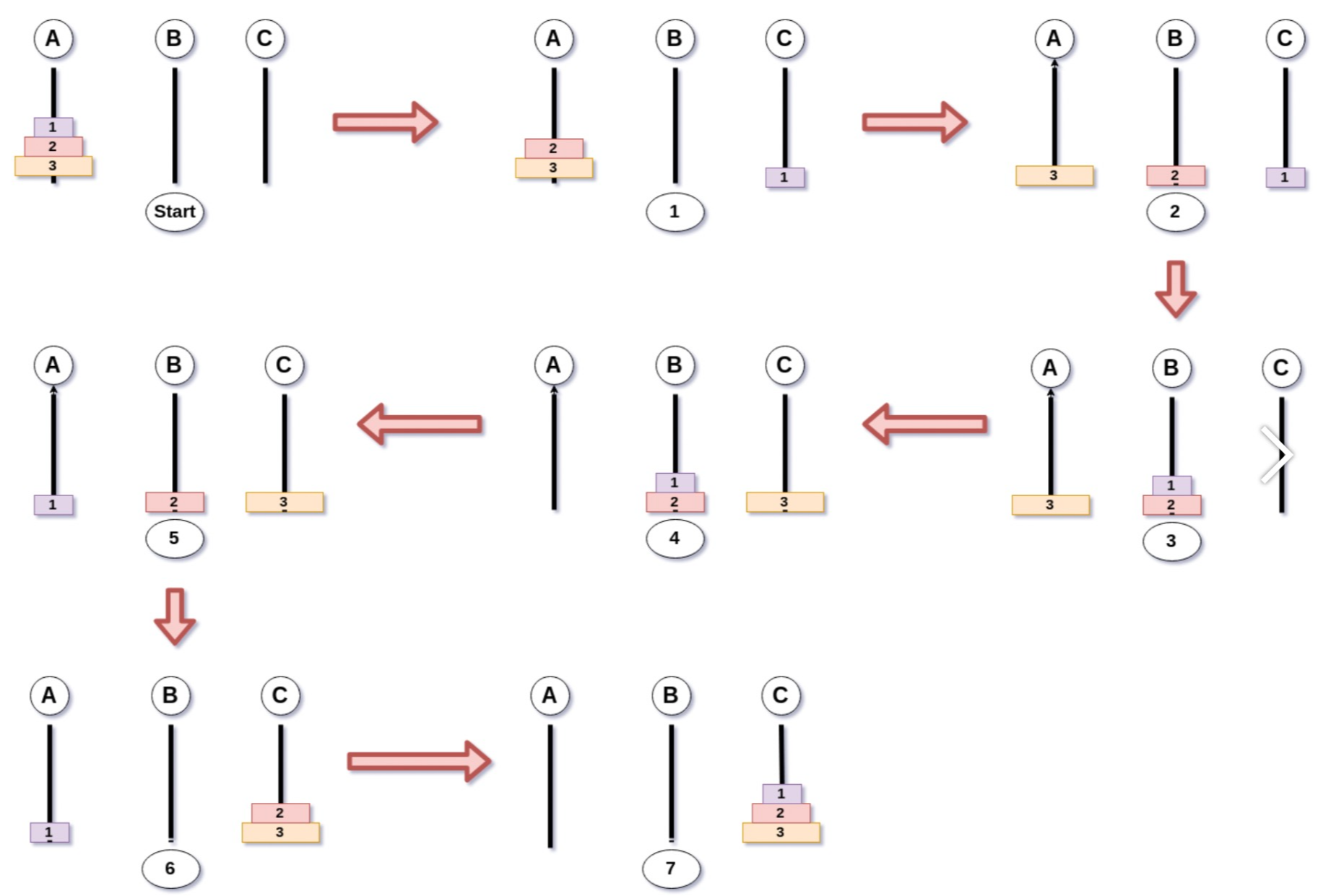
먼저 하노이 탑의 원판을 움직이려면 3개의 기둥이 있어야하며 a 기둥에 있는 원판을 c 기둥으로 옮기기 위해서는 거쳐야 하는 경유지 c 기둥이 항상 필요하다. 이때 시작하는 기둥을 start, 마지막으로 옮겨야 하는 목적지 기둥을 end, 경유지 기둥을 tmp라고 하자.

시작하는 기둥: start, 목적지 기둥: end, 경유지 기둥: tmp

 

 

[A] 다음 정의에 따르면 n개의 원판을 가진 하노이탑(H)은 결국 H(n start,end,tmp)의 함수로 정의된다.

이는 start->tmp->end를 의미한다.

 

다시 돌아와 3(N)개의 기둥에 3개의 원판이 꽂힌 상태를 상상해 보자. (위 그림 참조)

 

① 먼저 맨 위의 두 개의 원판(N-1)이 'B'로 이동해야 한다. 이동 후 그림은 3번이며 경유지를 거치는 모습은 1,2번으로 설명된다.

② 3번 그림에서 남은 하나의 기둥은 곧 바로 목적지인 'C'로 이동한다.

③ 4번 그림에서 ①번에서 다룬 두 개의 원판(N-1)은 'C'로 이동해야 한다. 이동 후 그림은 7번이며 경유지를 거치는 모습은 5,6번으로 설명된다.

 

[B] 자 여기서 규칙을 찾을 수 있다. ①과 ③번의 구조가 비슷하다. 정확히 말하면 'C'로 이동하는 것은 같으나 출발지, 경유지, 도착지가 다르다. 여기서 이 문제의 가장 큰 해답을 얻을 수 있다.

1. 첫 재귀에서 맨 밑 N번째 원판을 도착지 'C'로 이동을 위해 (N-1)개를 경유지로 이동한다.
2. 경유지에 도착한 (N-1)개의 원판을 목적지로 이동한다.

 

[C] [A]에서 우리는 함수를 H(n start,end,tmp)로 정의했다. 그리고 [B]에서 (함수 내에서) 재귀가 두번이 필요하며 두 재귀의 인자 순서가 다르다는 것을 알았다. 그러면 [A] 함수의 인자를 기준으로 [B] 재귀함수에 사용되는 인자를 배치하면 다음과 같다.

그림으로 표현하면 다음과 같다. 아래는 생략한다.

 

void hanoi(int n, int start, int end, int tmp) /*생략*/ hanoi(n-1,start,tmp,end); printf("[%d]->[%d]\n",start,end); hanoi(n-1,tmp,end,start);

[D] 마지막으로 남은 1개의 원판은 바로 'C'로 이동하므로 재귀가 필요하지 않는다. 따라서 출력함수만 작성한다

[ 알고리즘 분석 ]

[A]~[D]의 알고리즘에 따라 코드를 작성하면 아래와 같다. 생각보다 간결한 모습을 보여준다.

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
int rst = 0;
void hanoi(int n, int start, int end, int tmp){
    rst ++;
    if(n==1) printf("[%d]->[%d]\n",start,end);
    else{
        hanoi(n-1,start,tmp,end);
        printf("[%d]->[%d]\n",start,end);
        hanoi(n-1,tmp,end,start);
    }
}
int main(){
    int num; 
    printf("탑의 개수를 입력하세요: ");scanf("%d",&num); 
    hanoi(num,1,3,2);
    printf("재귀 횟수: %d",rst);
}

하노이의 탑 알고리즘은 아래 블로그를 참조했다.

'하노이의 탑' 이해하기 (feat. 재귀 함수)