[모두의 딥러닝] #2. 딥러닝의 동작원리
3장 가장 훌륭한 예측선 긋기 : 선형회귀
1. 선형 회귀
회귀는 데이터를 이용해 입력 변수(독립 변수)와 결과 값(종속 변수) 사이의 관계를 찾아내는 방법이다.
회귀(Regression)는 데이터에서 변수들 간의 관계를 모델링하여, 독립 변수(입력 변수)를 기반으로 종속 변수(출력 변수)를 예측하는 통계적 방법이다. 회귀 분석은 주로 연속적인 값을 예측하는 데 사용되며, 머신러닝의 기본적인 지도 학습 기법 중 하나로 자리 잡고 있다.
회귀의 주요 목표는 입력 변수와 출력 변수 간의 수학적 관계를 찾아내어, 새로운 데이터가 주어졌을 때 출력 값을 정확하게 예측하는 것으로, 쉽게 말해 "입력값이 이럴 때 결괏값은 이런 경향이 있다"라는 관계를 찾아내는 것이다. 예를 들어, 공부 시간에 따라 시험 점수가 달라진다고 하면, 공부 시간을 입력값으로 넣으면 점수를 예측할 수 있게 해주는 것이다.
선형 회귀는 이 관계를 직선으로 표현하는 방법이다. 공부 시간이 늘어나면 점수도 꾸준히 올라가는 상황을 상상하면 된다. 그래프 위에 직선을 그려서, 주어진 시간에 해당하는 점수를 예측한다. 다중 회귀는 예측에 필요한 조건이 여러 개일 때 사용한다. 예를 들어, 집값을 예측하려면 집의 크기, 위치, 방의 개수 같은 여러 요소를 고려해야 한다. 이 경우에는 단순한 직선이 아니라 여러 요소를 합쳐서 관계를 설명한다.
2. 가장 훌륭한 예측선이란?
선형 회귀란 정확한 직선을 그려내는 것 = 최적의 a와 b값을 찾는 것
3. 최소 제곱법
최소 제곱법은 딥러닝에서 최소 제곱법은 주로 회귀 분석에서 사용되는 손실 함수의 하나이다.
최소 제곱법은 예측값과 실제값 사이의 차이를 제곱하여 그 합을 최소화하는 방법으로, 예측 오차를 최소화하기 위한 대표적인 손실 함수로 사용됩니다.
최소제곱법은 주어진 x의 값이 하나일 때(단순선형회귀) 일 때 적용이 가능하며, 여러 개의 x가 주어지는 경우 경사 하강법을 이용한다.
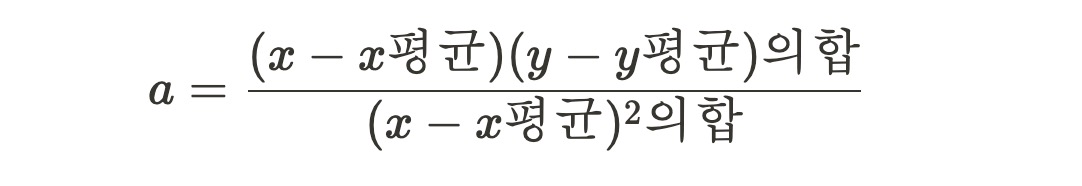
y 절편을 구하는 방법은 아래와 같다.

최소 제곱법을 통해 오차가 가장 적은 주어진 좌표의 특성을 가장 잘 나타내는 직선을 얻을 수 있다.
이때 얻은 직선이 요구되는 예측 직선으로, 이 직선을 통해 다른 데이터를 입력하여 예측값을 얻을 수 있다.
4. 코딩으로 확인하는 최소 제곱
아래는 NumPy에서 자주 사용하는 함수들을 표로 정리한 내용이다. 이중에서 가장 빈번하게 사용되는 함수를 강조했다.
| 함수 이름 | 함수 인자 | 함수 설명 | 예시 |
| np.array | iterable, dtype=None, copy=True | 리스트나 튜플 등을 배열로 변환 | np.array([1, 2, 3]) → array([1, 2, 3]) |
| np.zeros | shape, dtype=float | 주어진 크기의 0으로 채워진 배열 생성 | np.zeros((2, 3)) → array([[0., 0., 0.], [0., 0., 0.]]) |
| np.ones | shape, dtype=float | 주어진 크기의 1로 채워진 배열 생성 | np.ones((2, 3)) → array([[1., 1., 1.], [1., 1., 1.]]) |
| np.arange | start, stop, step, dtype=None | 특정 범위 내에서 일정 간격으로 값을 생성 | np.arange(0, 5, 1) → array([0, 1, 2, 3, 4]) |
| np.linspace | start, stop, num=50, endpoint=True | 시작과 끝 사이를 균등하게 나누어 값 생성 | np.linspace(0, 1, 5) → array([0., 0.25, 0.5, 0.75, 1.]) |
| np.reshape | array, newshape | 배열의 형태를 변경 | np.reshape(np.arange(6), (2, 3)) → array([[0, 1, 2], [3, 4, 5]]) |
| np.transpose | array, axes=None | 배열의 차원을 전치 | np.transpose([[1, 2], [3, 4]]) → array([[1, 3], [2, 4]]) |
| np.dot | a, b | 두 배열의 내적 계산 | np.dot([1, 2], [3, 4]) → 11 |
| np.sum | array, axis=None, dtype=None | 배열의 모든 요소 또는 특정 축의 합 계산 | np.sum([[1, 2], [3, 4]]) → 10 |
| np.mean | array, axis=None, dtype=None | 배열의 평균 계산 | np.mean([1, 2, 3, 4]) → 2.5 |
| np.std | array, axis=None, dtype=None | 배열의 표준 편차 계산 | np.std([1, 2, 3, 4]) → 1.118 |
| np.max | array, axis=None | 배열의 최댓값 계산 | np.max([[1, 2], [3, 4]]) → 4 |
| np.min | array, axis=None | 배열의 최솟값 계산 | np.min([[1, 2], [3, 4]]) → 1 |
| np.argmax | array, axis=None | 배열에서 최댓값의 인덱스를 반환 | np.argmax([1, 3, 2]) → 1 |
| np.argmin | array, axis=None | 배열에서 최솟값의 인덱스를 반환 | np.argmin([1, 3, 2]) → 0 |
| np.sort | array, axis=-1 | 배열의 요소를 정렬 | np.sort([3, 1, 2]) → array([1, 2, 3]) |
| np.concatenate | arrays, axis=0 | 여러 배열을 주어진 축을 따라 연결 | np.concatenate([[1, 2], [3, 4]], axis=0) → array([1, 2, 3, 4]) |
| np.stack | arrays, axis=0 | 여러 배열을 새로운 축으로 쌓음 | np.stack([[1, 2], [3, 4]], axis=1) → array([[1, 3], [2, 4]]) |
| np.unique | array, return_index=False, return_counts=False | 배열에서 중복 제거 후 고유값 반환 | np.unique([1, 2, 2, 3]) → array([1, 2, 3]) |
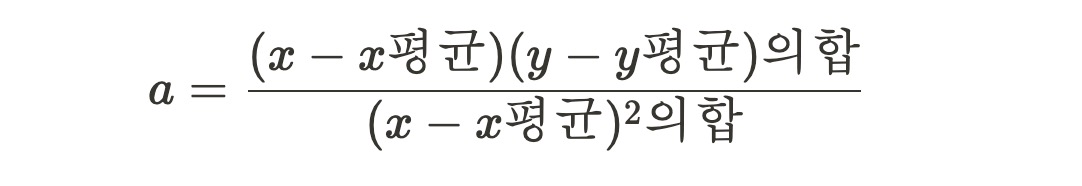
최소 제곱근 공식에서 'x의 각 원소와 x의 평균값들의 차를 제곱'은 div로 표현된다. 이미지의 분모에 해당한다.
분자에는 x와 x평균, y와 y평균 즉 4가지의 인자가 필요하다. 이는 함수를 선언하여 계산하고 반환값을 사용한다.
denominator = sum([(i - mx)**2 for i in x]) #x의 각 원소와 x의 평균값들의 차를 제곱(분모)
def calculate_Numerator(x, mx , y, my):
rst = 0
# (x-x평균)(y-y평균)의 합
for i in range( len(x) ):
rst += (x[i]-mx)*(y[i]-my)
return rst
Numerator = calculate_Numerator(x,mx,y,my) #분자
기울기(a)는 분자와 분모의 비율이며, 절편(b)는 앞선 공식과 동일하게 계산한다.

a = Numerator / denominator
b = my - (mx*a) #y의 평균 - (x의 평균 * 기울기 a)x의 평균값 : 5.0
x의 평균값 : 90.5
분모 : 20.0
분모 : 46.0
기울기 : 2.3
절편 : 79.0
5. 평균 제곱 오차
앞서 실행해본 최소제곱법은 데이터를 설명하는 최적의 직선을 찾는 선형적 방법이다.
이 방법은 관측된 데이터와 모델이 예측한 값 사이의 차이를 나타내는 오차의 제곱합을 최소화하는 방향으로 작동한다. 이를 통해 직선의 기울기와 절편을 결정하며, 회귀 분석에서 주로 사용된다.
최소제곱법은 간단하고 직관적이지만, 몇 가지 단점과 한계를 가지고 있다.
1. 이상치(Outlier)에 민감하다
오차의 제곱합을 사용하기 때문에 데이터에 이상치가 포함되면 모델이 큰 영향을 받는다.
이상치가 한두 개만 있어도 최적의 직선이 왜곡될 수 있다.
2. 비선형 관계를 설명하지 못함
최소제곱법은 선형 모델을 가정하기 때문에 독립 변수와 종속 변수 사이의 비선형 관계를 설명할 수 없다.
따라서 비선형 데이터에는 적합하지 않다.
3. 잔차의 정규성 및 등분산성 가정
최소제곱법은 잔차(Residual)가 정규분포를 따르고 분산이 일정해야 한다는 가정을 전제로 한다.
이 가정이 깨지면 결과의 신뢰성이 낮아질 수 있다.
4. 고차원 데이터에서의 과적합
다중 회귀 분석 등에서 변수가 많아지면 최소제곱법이 과적합 문제를 일으킬 가능성이 있다.
이는 모델이 학습 데이터에 지나치게 적합되어 테스트 데이터에 대한 일반화 능력이 떨어지는 현상을 초래한다.
평균제곱오차(MSE)의 개념
평균제곱오차(Mean Squared Error, MSE)는 예측 값과 실제 값 간의 차이를 제곱하여 평균을 구한 값이다. 이는 모델의 성능을 평가하기 위한 지표로 널리 사용된다. 공식은 다음과 같다: ( : 실제 값 / y^_: 예측 값 / : 데이터의 개수)

MSE가 필요한 이유
MSE는 모델 성능을 정량적으로 평가하고 최적화를 가능하게 만드는 핵심 도구이다. 이를 사용하는 이유는 다음과 같다.
| 오차 직관적 파악 | MSE는 오차의 크기를 제곱한 값으로 계산하므로, 양수로만 표현되어 오차의 크기를 직관적으로 이해하기 쉽다. |
| 큰 오차에 민감한 지표 | MSE는 오차를 제곱하기 때문에 큰 오차에 더 큰 패널티를 부여한다. 이는 이상치가 큰 영향을 미치는 경우, 모델을 개선해야 할 필요성을 쉽게 파악하게 해준다. |
| 평가 기준의 표준화 | MSE는 다양한 모델의 성능을 비교하는 데 유용하다. 수치적으로 작을수록 좋은 모델임을 명확히 나타내므로, 모델 간의 객관적인 비교가 가능하다. |
| 미분 가능성 | MSE는 수학적으로 미분 가능하므로 경사하강법(Gradient Descent)과 같은 최적화 알고리즘에 쉽게 활용할 수 있다. 이는 딥러닝과 머신러닝 모델의 학습 과정에서도 필수적이다. |
MSE의 단점과 최소제곱법의 한계를 보완하기 위해 다양한 접근법이 활용된다. 예를 들어, 이상치의 영향을 줄이기 위해 평균절대오차(MAE)나 Huber Loss를 사용할 수 있으며, 비선형 데이터를 처리하기 위해 비선형 회귀 모델이나 신경망 모델을 적용할 수 있다.
6. 잘못 그은 선 바로잡기
모든 딥러닝 프로젝트는 여러 개의 변수를 사용하므로, 여러 입력 데이터가 입력 가능하며 비선형 관계를 다룰 수 있어야 한다.
이를 위해 가설을 세운 후 이 가설이 주어진 요건을 충족하는지 판단하여 조금씩 변화시키는 방법을 사용한다.
가설의 결과가 긍정적이면 오차가 최소가 될 때까지 이 과정을 반복한다. 이는 딥러닝에서 가장 중요한 원리이다.
이를 위해서는 이전에 그린 '선'보다 가장 최근에 그린 '선'이 긍정적임을 판단하는 근거가 필요하다. 조건을 정리하면 아래와 같다.
1. 각 선의 오차를 구할 수 있어야 한다.
2. 오차가 작은 쪽으로 변경해야 한다.
앞선 데이터를 활용하여 '최소제곱법'이 아니라 무작위 선을 그리고 오차를 줄이는 방식을 사용해 보자.
임의의 직선의 오차는 각 점과 그래프 간의 수직 거리를 확인하면 된다. 이 합이 작을수록 잘 그린 선이라고 판단할 수 있다!
이때 임의의 직선과 각 점의 수직거리 차이는 양수와 음수 모두 될 수 있다.
이로 인해 오차(=임의의 직선과 각 점의 수직거리 차이의 합) 또한 양수와 음수가 될 수 있으므로 해당 오차를 통해 실제 오차가 얼마나 큰 지 판단하기 어렵다. 이를 위해 오차의 합을 구할 때 각 오차의 값(실제값 - 직선의 거리)을 제곱하여 더한다
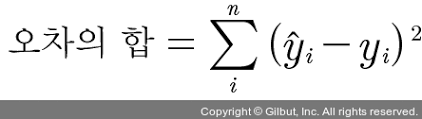
위 식에서 얻은 오차의 합을 n으로 나누면 오차 합의 평균을 구할 수 있는데, 이를 평균 제곱 오차라고 한다.
평균 제곱 오차를 통해 오차의 결과가 가장 작은 선을 찾아야 한다.
임의의 직선을 긋고, 이에 대한 평균 제곱 오차를 구한 후 이 값을 가장 작게 만드는 a와 b를 찾는 과정이 바로 선형 회귀이다.
7. 코딩으로 확인하는 평균 제곱 오차
이번에는 data라는 리스트를 만들어 공부한 시간과 이에 따른 성적을 나누어 저장한다.
즉 독립변수에 따른 종속변수를 하나의 배열에 저장한다.
#x = [2,4,6,8]
#y = [81 , 93, 91, 97]
data = [[2,81] , [4,93] , [6,93] ,[8,97]] #(x1,y1) , (x2,y2) ,,,
x = [ i[0] for i in data]
y = [ i[1] for i in data]
다음으로 임의의 직선 변수를 적용한 선과 최소 제곱 오차 공식을 코드로 작성한다.
tmp_a_b = [3, 76] # 임의의 직선 변수
#최소제곱법으로 구한 실제 직선 변수 a(기울기) : 2.3
#최소제곱법으로 구한 실제 직선 변수 b(절편) : 79.0
# 임의의 tmp 값을 적용한 선
def tmp_line(x):
tmp_line_rst = tmp_a_b[0]*x + tmp_a_b[1]
return(tmp_line_rst)
# y : x에 대응하는 값
# y_h : x에 대응하는 임의의 직선의 값
def mse(y, y_h):
return (( (y - y_h)**2 ).mean()) #최소 제곱 오차 공식
# predict_result : 앞서 만든 일차 방정식 함수 tmp_line_rst의 값이 들어가게됨.
def mse_rst(y, tmp_line_rst):
return mse(np.array(y), np.array(tmp_line_rst))
함수가 설계가 끝났다면 예측값이 들어갈 빈 리스트와 모든 x에 저장된 값들 한 번씩 임의로 생성된 예측 직선에 대입하여 공부시간과 실제 점수 간의 예측값을 비교한다.
predict_result = []
for i in range(len(x)):
predict_result.append(tmp_line(x[i]))
print("공부시간 : %.f, 실제 점수 : %.f, 예측 점수 : %.f" %(x[i],y[i],tmp_line(x[i])))공부시간 : 2, 실제 점수 : 81, 예측 점수 : 82
공부시간 : 4, 실제 점수 : 93, 예측 점수 : 88
공부시간 : 6, 실제 점수 : 91, 예측 점수 : 94
공부시간 : 8, 실제 점수 : 97, 예측 점수 : 100

앞서 설명했듯, 평균제곱오차(MSE)는 모델이 예측한 값과 실제 값 사이의 차이를 수치적으로 나타내는 평가 지표이다. 쉽게 말해, "모델이 얼마나 틀렸는지"를 나타내는 척도이다. 이 값이 작을수록 모델의 예측이 실제 값과 가까워진다.
MSE는 각 데이터 포인트에서 실제 값과 예측 값 간의 차이를 구한 뒤, 이를 제곱하여 평균을 낸 값이다. 이때 제곱을 하는 이유는 오차가 양수와 음수로 섞여 있을 때 서로 상쇄되지 않도록 하기 위함이다. MSE를 통해 직선이 데이터를 얼마나 잘 설명하는지 알 수 있으며, 기울기 w와 절편 b를 조정하여 MSE를 최소화하면 가장 적합한 예측 직선을 얻을 수 있다.
쉽게 설명하자면, MSE는 데이터와 예측 간의 "평균적인 거리"를 측정한다고 생각하면 된다.
모델이 예측을 잘못할수록 MSE 값이 커지고, 예측이 정확할수록 값이 작아진다. 예측 직선을 개선하는 목표는 바로 이 평균적인 거리를 줄이는 것이다. 딥러닝에서도 MSE는 비슷한 원리로 사용되며, 네트워크의 가중치와 편향(딥러닝에서 직선의 기울기와 절편에 해당)을 조정해 예측을 점점 더 정확히 만들어가는 과정에 사용된다.
4장. 오차 수정하기 : 경사 하강법
앞서 기울기에 따라 오차의 값이 변동된다는 것을 확인했다.
다시 말해 a가 무한대에 근접하면 오차도 무한대에 근접하며 무한대로 작게 해도 오차는 무한대로 커진다. 이는 이차함수로 표현 가능하다.
이차 함수(아래 볼록)에서 가장 작은 값은 당연하게도 그래프의 가장 아래 볼록한 부분이다.
주목해야 할 점은 이 부분이 바로 기울기가 0인 부분이라는 것이다! 그렇다면 아래 고민이 생긴다.
그렇다면 이 기울기가 0인 부분, 오차가 가장 작은 부분을 구하기 위해서 어떻게 해야 할까?
간단하다.
1. 컴퓨터를 이용해 임의의 한 점을 찍는다.
2. (1)에서 찍은 한 점을 기울기가 0인 부분, m에게 근접하도록 이동시킨다.
하지만 여전히 고민이 생긴다!
어떻게 컴퓨터가 임의의 점 a가 m에 가까운 것을 판단할 것인가?
이를 해결하기 위해 경사하강법이 필요하다.
1. 경사 하강법의 개요
미분은 해당 지점의 기울기이다. 이를 이용해 임의의 점 a의 미분을 구하고 이 값이 0인 지점을 m으로 여길 수 있다. 따라서 우리는 m 지점을 찾기 위해서 미분이 0인 지점을 찾아야 한다.
1. 임의의 지점 a의 미분을 구한다.
2. 미분의 값(기울기)이 음수인 경우 이는 m의 좌측에 있음을 의미하므로 양의 방향으로 이동시킨다.
3. 미분의 값(기울기)가 양수인 경우, 이는 m의 우측에 있음을 의미하므로 음의 방향으로 이동한다.
4. 1~3의 과정을 반복하여 기울기가 0인 m 지점을 찾는다.
위 방법을 통해 반복적으로 기울기 a을 변화시켜 m의 값을 찾아내는 것이 바로 경사하강법이다.
2. 학습률
경사하강법에서 부호에 따라 임의의 지점 a를 이동할 때, 적절한 거리를 이동하지 않는 경우 값이 한 점으로 수렴하지 않는다.
따라서 거리를 이동할때 얼마큼 이동할지가 중요하며, 이때 이동 거리를 지정하는 것이 바로 학습률이다.
즉, 경사 하강법은 오차의 변화에 따라 이차 함수 그래프를 만들 때 적절한 학습률을 구해 미분 값이 0인 지점을 구하는 것이다.
이때 b의 값에 따라 오차가 변화므로 최적의 b값을 결정할때 역시 경사하강법을 이용한다.
3. 코딩으로 확인하는 경사 하강법
이제 경사 하강법을 구현하여 평균제곱오차(MSE)를 최소화하는 최적의 기울기(a)와 절편(b)을 찾아보자. 목표는 데이터를 설명하는 예측 직선을 점점 더 정확히 만들어가는 것이다. 경사 하강법의 핵심은 현재의 기울기와 절편을 조금씩 조정하며 MSE를 줄이는 것이다.
우선 이전과 동일한 데이터를 사용한다.
data = [[2, 81], [4, 93], [6, 91], [8, 97]]
x = np.array([i[0] for i in data]) # 공부 시간
y = np.array([i[1] for i in data]) # 실제 점수
앞선 평균 제곱 오차에서 y_h는 x에 대응하는 임의의 직선의 값이라고 했다. 따라서 평균 제곱 오차에 y_h에 임의의 직선의 방정식 tmp_line를 적용해도 무방하다.
하지만 우리가 유의할 점은 따로 있다.
경사하강법은 반복적으로 기울기 a을 변화시켜 m의 값을 찾아내는 것으로, 다시 말해 기울기와 절편만 편미분해야한다!
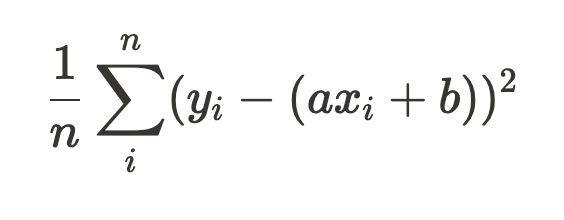 |
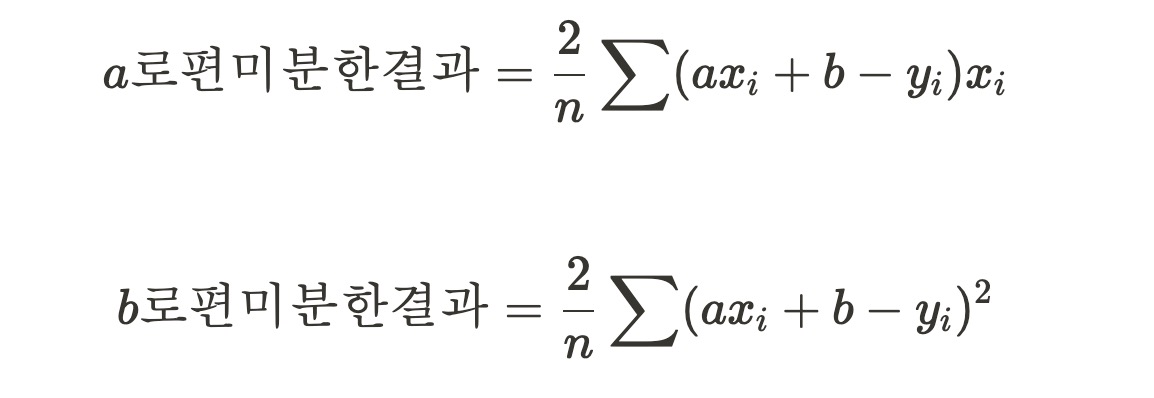 |
이를 코드로 나타내면 다음과 같다.
데이터 구축
import pandas as pd
import matplotlib.pyplot as plt
x_data = np.array(x) #리스트로 변환하여 계산이 용이
y_data = np.array(y)
pandas는 데이터를 다루기 위한 라이브러리로, 표 형태의 데이터를 읽고 쓰며 조작할 수 있도록 도와준다. 데이터프레임(DataFrame)과 시리즈(Series)를 활용해 데이터를 정리, 분석, 처리하는 데 사용된다.
matplotlib.pyplot는 데이터 시각화를 위한 라이브러리로, 다양한 형태의 그래프를 그릴 수 있다. 선 그래프, 막대그래프, 산점도 등 데이터를 직관적으로 표현하는 데 사용된다.
# 초기 기울기와 절편
a = 0 # 초기 기울기
b = 0 # 초기 절편
# 학습률
learning_rate = 0.03
# 반복 횟수
epochs = 2001기울기와 절편은 직선을 정의하는 기본 요소로 여기서 a는 초기 기울기를 나타내며, 0으로 설정하여 학습의 시작점을 정한다. b는 초기 절편으로, 마찬가지로 0으로 설정하여 초기 직선을 단순화한다.
학습률(learning rate)은 경사 하강법에서 얼마나 빠르게 값을 조정할지를 결정하는 중요한 변수이다. 학습률을 0.03으로 설정하면, 반복마다 기울기와 절편이 작은 단계로 조정되어 안정적인 학습을 보장한다.
반복 횟수(epochs)는 학습이 몇 번 이루 어질지를 의미하며, 2001번으로 설정하여 충분히 많은 반복을 통해 최적의 기울기와 절편을 찾는다. 학습 과정은 각 반복에서 기울기와 절편이 점차 조정되어 오차를 최소화하는 방향으로 진행된다.
경사하강법 실행
경사 하강법 실행 코드는 주어진 데이터를 반복적으로 학습하며 기울기와 절편을 조정하여 오차를 최소화한다.
반복문 안에서 다음 과정을 수행한다:
1. 현재 기울기와 절편을 사용해 예측 값을 계산한다.
2. 예측 값과 실제 값의 차이를 계산하여 오차를 구한다.
3. 평균제곱오차(MSE)의 편미분을 계산하여 기울기와 절편에 대한 그래디언트를 구한다.
- gradient_a는 기울기에 대한 그래디언트이며, 데이터 크기와 학습률에 따라 조정된다.
- gradient_b는 절편에 대한 그래디언트이다.
4. 기울기와 절편을 학습률을 기반으로 업데이트한다.
5. 특정 횟수마다 현재 상태를 출력하여 학습 과정을 확인한다. 평균제곱오차(MSE)도 함께 출력된다.
이 과정은 반복 횟수(epoch) 동안 실행되며, 각 반복에서 기울기와 절편이 점진적으로 최적화된다.
편미분 알고리즘
기울기에 대한 편미분은 예측 값이 실제 값과 얼마나 차이 나는지를 각 데이터의 x 값과 연관시켜 계산한다.
이는 기울기가 오차에 미치는 영향을 나타낸다.
gradient_a = -(2 / len(x)) * sum(x * (y - y_pred)) #오차 함수를 a로 미분한 값
a -= learning_rate * gradient_a #학습률을 곱해 기존의 값 업데이트
위 식은 각 데이터의 x 값과 오차의 곱을 평균 내어 기울기에 대한 편미분을 계산한다. 2로 나누는 이유는 평균제곱오차의 제곱에 따른 미분 특성 때문이다. 절편에 대한 편미분은 데이터의 x 값과 상관없이 오차의 평균을 계산하여 절편이 오차에 미치는 영향을 나타낸다.
gradient_b = -(2 / len(x)) * sum(y - y_pred) #오차 함수를 b로 미분한 값
b -= learning_rate * gradient_b #학습률을 곱해 기존의 값 업데이트
이 식은 오차의 합을 평균 내어 절편에 대한 그래디언트를 구한다.
결국, 편미분은 현재 기울기와 절편이 얼마나 수정되어야 오차를 줄일 수 있을지를 수치적으로 계산한다.
이 값은 경사 하강법에서 기울기와 절편을 업데이트하는 데 사용된다.
| y_pred = a * x_data + b |
|
 |
gradient_a = -(2 / len(x)) * sum(x * (y - y_pred)) |
| gradient_b = -(2 / len(x)) * sum(y - y_pred) | |
코드의 편미분 계산과 첨부된 이미지의 편미분 식이 다르게 보이는데 이는 아래의 차이점에서 기인한다.
코드에서 y−y_pred를 사용한 반면, 이미지에서는 ax+b−y를 사용했다. 이는 오차를 계산하는 기준의 부호 차이에서 비롯된 것으로, 아래와 같이 두 식은 동일하다. 다만 빼는 위치가 역순이므로 마이너스가 붙는다.
- : 실제 값에서 예측 값을 뺌 (코드 표현)
- : 예측 값에서 실제 값을 뺌 (이미지 표현)
따라서 부호만 다르기 때문에 계산 결과는 동일하다는 것을 확인할 수 있다.
# 경사 하강법 실행
for i in range(epochs):
y_pred = a * x_data + b #임의의 직선 함수에 x데이터 행렬 대입
error = y_data - y_pred
# 기울기(a)와 절편(b)에 대한 MSE의 편미분 계산
gradient_a = -(2 / len(x)) * sum(x * (y - y_pred))
gradient_b = -(2 / len(x)) * sum(y - y_pred)
# 기울기와 절편 업데이트
a -= learning_rate * gradient_a
b -= learning_rate * gradient_b
# 매 100번 반복마다 학습 상태 출력
if i % 100 == 0:
mse = np.mean((y - y_pred) ** 2)
print(f"Epoch {i}: a = {a:.4f}, b = {b:.4f}, MSE = {mse:.4f}")Epoch 0: a = 27.8400, b = 5.4300, MSE = 8225.0000
Epoch 100: a = 7.0739, b = 50.5117, MSE = 146.2553
Epoch 200: a = 4.0960, b = 68.2822, MSE = 27.8259
Epoch 300: a = 2.9757, b = 74.9678, MSE = 11.0637
Epoch 400: a = 2.5542, b = 77.4830, MSE = 8.6912
Epoch 500: a = 2.3956, b = 78.4293, MSE = 8.3554
Epoch 600: a = 2.3360, b = 78.7853, MSE = 8.3078
Epoch 700: a = 2.3135, b = 78.9192, MSE = 8.3011
Epoch 800: a = 2.3051, b = 78.9696, MSE = 8.3002
Epoch 900: a = 2.3019, b = 78.9886, MSE = 8.3000
Epoch 1000: a = 2.3007, b = 78.9957, MSE = 8.3000
Epoch 1100: a = 2.3003, b = 78.9984, MSE = 8.3000
Epoch 1200: a = 2.3001, b = 78.9994, MSE = 8.3000
Epoch 1300: a = 2.3000, b = 78.9998, MSE = 8.3000
Epoch 1400: a = 2.3000, b = 78.9999, MSE = 8.3000
Epoch 1500: a = 2.3000, b = 79.0000, MSE = 8.3000
Epoch 1600: a = 2.3000, b = 79.0000, MSE = 8.3000
Epoch 1700: a = 2.3000, b = 79.0000, MSE = 8.3000
Epoch 1800: a = 2.3000, b = 79.0000, MSE = 8.3000
Epoch 1900: a = 2.3000, b = 79.0000, MSE = 8.3000
Epoch 2000: a = 2.3000, b = 79.0000, MSE = 8.3000
학습한 기울기와 절편을 시각화하면 다음과 같다.
y_pred = a * x_data + b
plt.scatter(x,y)
plt.plot( [min(x_data),max(x_data)],[min(y_pred),max(y_pred)])
plt.show()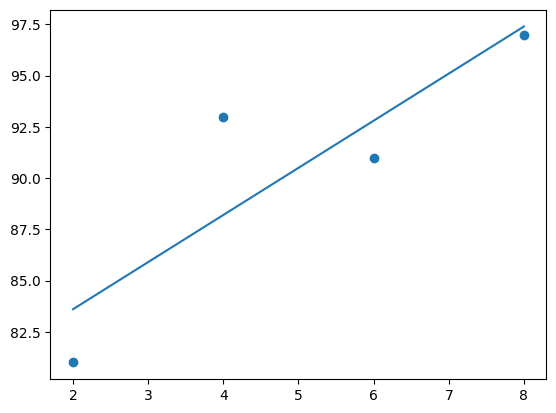
4. 다중 선형 회귀
다중 선형회귀는 독립 변수가 여러 개인 경우에 사용하는 회귀 분석 기법이다.
회귀는 데이터를 이용해 입력 변수(독립 변수)와 결과 값(종속 변수) 사이의 관계를 찾아내는 방법이다.
단순 선형회귀가 하나의 독립 변수와 하나의 종속 변수 간의 관계를 모델링하는 반면, 다중 선형회귀는 여러 독립 변수와 하나의 종속 변수 간의 관계를 모델링한다. 다중 선형회귀는 다음과 같은 수학적 형태로 표현된다:
y = b0 + b1 * x1 + b2 * x2 +... + bn * xn + e
• y: 종속 변수(예측하려는 값)
• b0: 절편
• b1, b2,..., bn: 독립 변수에 대한 회귀 계수(기울기)
• x1, x2,..., xn: 독립 변수(입력 변수)
• e: 오차(예측 값과 실제 값의 차이)
다중 선형회귀의 필요성
단순 선형 회귀는 기존 요소를 제외한 다른 요소가 결과에 미치는 영향을 반영할 수 없다.
따라서 더 정확한 예측을 위해서는 추가 정보를 입력해야 하며, 추가한 정보를 반영해 새로운 예측을 하기 위해 다중 선형회귀가 필요하다.
1. 현실 세계의 복잡한 데이터 설명 : 단순 선형회귀는 하나의 변수만 고려하기 때문에 다중 선형회귀가 필요하다.
2. 변수 간 상호작용 반영 : 여러 독립 변수가 종속 변수에 개별적/동시 영향을 미치는 관계를 모델링할 수 있음.
3. 더 정확한 예측 가능 : 모델이 종속 변수를 더 정확히 설명할 수 있음.
4. 통계적 분석과 의사결정 지원: 각 독립 변수의 기여도를 수치화하여 어떤 변수가 결과에 더 큰 영향을 미치는지 파악 가능.
5. 다차원 데이터를 다룰 수 있음: 2차원 이상의 데이터를 처리 가능, 고차원 문제에서도 유용함.
5. 코딩으로 확인하는 다중 선형 회귀
"2-4. 코딩으로 구현하는 최소제곱법"과 다른 새로운 주피터 노트북을 이용한다.
입력 데이터 세트(배열)를 선언한다. 이번에는 독립변수(x)가 2개인 배열을 선언한다.
이 데이터 세트를 시각화하기 위해 mplot3 d 라이브러리를 이용한다.
data = [[2, 0, 81], [4, 4, 93], [6, 2, 91], [8, 3, 97]]
x1 = [i[0] for i in data] #study_hours : 공부한 시간
x2 = [ i [1] for i in data] #private_class : 과외시간
y = [ i[2] for i in data] # Score1 : 성적mplot3d 라이브러리
mplot3 d 라이브러리는 Matplotlib의 확장 모듈로, 3차원 데이터를 시각화하는 데 사용된다. 이를 통해 2D 플롯뿐만 아니라 3D 공간에서 데이터를 효과적으로 표현할 수 있다. 주요 역할은 3차원 축을 생성하고 이를 활용해 선 그래프, 산점도, 표면 그래프, 막대그래프, 등고선 그래프 등을 그리는 것이다. 또한, 그래프의 각도를 조정하거나 축의 범위를 설정하고 색상 맵과 투명도를 적용하여 시각적인 정보를 더욱 명확히 전달할 수 있다
자주 사용하는 함수를 강조 표시하였다.
| 기능 | 사용법 | 설명 |
| 3D 축 생성 | ax = plt.axes(projection='3d') | 3D 플롯을 그리기 위한 축을 생성 |
| 3D 선 그래프 | ax.plot3D(x, y, z, color) | x, y, z 좌표를 이용한 3D 선 그래프 |
| 3D 산점도 | ax.scatter3D(x, y, z, c, cmap) 혹은 ax.scatter(x, y, z, c, cmap) |
x, y, z 좌표를 이용한 3D 산점도, 색상 맵(cmap)을 추가 가능 |
| 3D 표면 그래프 | ax.plot_surface(X, Y, Z, cmap) | X, Y 좌표 격자와 Z 값을 이용한 3D 표면 그래프 |
| 3D 등고선 그래프 | ax.contour3D(X, Y, Z, levels, cmap) | X, Y 좌표와 Z 값에 따른 등고선 생성 |
| 3D 막대 그래프 | ax.bar3d(x, y, z, dx, dy, dz) | x, y, z 위치에서 시작하는 3D 막대 그래프, 막대의 크기(dx, dy, dz) 설정 가능 |
| 3D 그래프 제목 설정 | ax.set_title(title) | 3D 플롯에 제목을 추가 |
| 3D 축 라벨 설정 | ax.set_xlabel(), ax.set_ylabel(), ax.set_zlabel() | 각각 x, y, z 축에 라벨 추가 |
| 3D 축의 범위 설정 | ax.set_xlim(), ax.set_ylim(), ax.set_zlim() | 각각 x, y, z 축의 범위를 설정 |
| 색상 및 스타일 설정 | cmap, color, alpha | 그래프의 색상 맵, 색상, 투명도 설정 |
| 보기 각도 설정 | ax.view_init(elev, azim) | 그래프를 표시하는 시점의 높이(elev)와 회전 각도(azim)를 설정 |
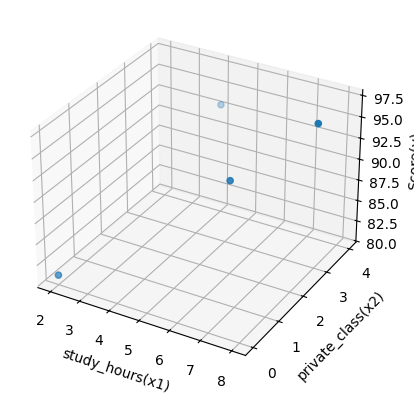
mplot3d 라이브러리를 이용한 데이터 시각화
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d # 3D 그래프 그리는 라이브러리 가져오기
ax = plt.axes(projection='3d')
ax.set_xlabel('study_hours(x1)' ) #x1
ax.set_ylabel('private_class(x2)') #x2
ax.set_zlabel('Score(y)') #y
ax.scatter(x1, x2, y)
plt.show()
출력 결과는 아래와 같다.
이제 x의 값이 두 개인, 다중 선형회귀이므로 각각의 기울기를 a1, a2로 만들어야 한다. 각각 앞서 진행한 경사하강법을 적용하고 학습률을 곱해 기존의 값을 업데이트한다.
입력 데이터 처리를 위해 아래 코드를 실행한다.
import numpy as np
x1_data = np.array(x1) #리스트로 변환하여 계산이 용이
x2_data = np.array(x2)
y_data = np.array(y)
# 초기 기울기와 절편
a1 = 0 # 초기 기울기
a2 = 0 # 초기 기울기
b = 0 # 초기 절편
# 학습률
learning_rate = 0.02
# 반복 횟수
epochs = 2001경사하강법과 학습률 적용
경사하강법과 학습률을 적용하기 위해 y를 구하는 식을 세운다. 이때 y = a1*x1 + a2*x2 + b로 표현되는 직선은 다중 선형회귀(Multiple Linear Regression) 모델에서 사용되는 2차원 평면 위의 직선이다. 이를 초평면(Hyperplane)이라고도 한다.
이때 2차원 평면 위의 직선에서 a1, a2, b를 각각 편미분 하고 경사하강법을 진행한 후, 학습률을 곱한다.
# 경사 하강법 실행
for i in range(epochs):
y_pred = a1 * x1_data + a2 * x2_data + b
# y를구하는식을세우기 : y = a1*x1 + a2*x2 + b (2차원 평면 위의 직선; 초평면)
error = y_data - y_pred # 오차(실제 y값과 예측직선간의 거리)
a1_diff = -(2/len(x1_data)) * sum(x1_data * (error)) #오차함수를 a1로 미분한값
a2_diff = -(2/len(x2_data)) * sum(x2_data * (error)) #오차함수를 a2로 미분한값
b_diff = -(2/len(x1_data)) * sum(y_data - y_pred) #오차함수를 b로 미분한 값
a1 = a1 - learning_rate * a1_diff # 학습률을 곱해 기존의 al 값 업데이트
a2 = a2 - learning_rate * a2_diff # 학습률을 곱해 기존의 a2 값 업데이트
b = b - learning_rate * b_diff # 학습률을 곱해 기존의 b 값 업데이트
# 매 100번 반복마다 학습 상태 출력
if i % 100 == 0:
mse = np.mean((y - y_pred) ** 2)
print(f"Epoch {i}: a1 = {a1:.4f}, a2 = {a2:.4f}, b = {b:.4f}, MSE = {mse:.4f}")Epoch 0: a1 = 18.5600, a2 = 8.4500, b = 3.6200, MSE = 8225.0000
Epoch 100: a1 = 7.2994, a2 = 4.2867, b = 38.0427, MSE = 260.7917
Epoch 200: a1 = 4.5683, a2 = 3.3451, b = 56.7901, MSE = 73.0672
Epoch 300: a1 = 3.1235, a2 = 2.8463, b = 66.7100, MSE = 20.5086
Epoch 400: a1 = 2.3591, a2 = 2.5823, b = 71.9589, MSE = 5.7934
Epoch 500: a1 = 1.9546, a2 = 2.4427, b = 74.7362, MSE = 1.6734
Epoch 600: a1 = 1.7405, a2 = 2.3688, b = 76.2058, MSE = 0.5200
Epoch 700: a1 = 1.6273, a2 = 2.3297, b = 76.9833, MSE = 0.1970
Epoch 800: a1 = 1.5673, a2 = 2.3090, b = 77.3948, MSE = 0.1066
Epoch 900: a1 = 1.5356, a2 = 2.2980, b = 77.6125, MSE = 0.0813
Epoch 1000: a1 = 1.5189, a2 = 2.2922, b = 77.7277, MSE = 0.0742
Epoch 1100: a1 = 1.5100, a2 = 2.2892, b = 77.7886, MSE = 0.0722
Epoch 1200: a1 = 1.5053, a2 = 2.2875, b = 77.8209, MSE = 0.0716
Epoch 1300: a1 = 1.5028, a2 = 2.2867, b = 77.8380, MSE = 0.0715
Epoch 1400: a1 = 1.5015, a2 = 2.2862, b = 77.8470, MSE = 0.0714
Epoch 1500: a1 = 1.5008, a2 = 2.2860, b = 77.8518, MSE = 0.0714
Epoch 1600: a1 = 1.5004, a2 = 2.2859, b = 77.8543, MSE = 0.0714
Epoch 1700: a1 = 1.5002, a2 = 2.2858, b = 77.8556, MSE = 0.0714
Epoch 1800: a1 = 1.5001, a2 = 2.2858, b = 77.8563, MSE = 0.0714
Epoch 1900: a1 = 1.5001, a2 = 2.2857, b = 77.8567, MSE = 0.0714
Epoch 2000: a1 = 1.5000, a2 = 2.2857, b = 77.8569, MSE = 0.0714
아래는 학습한 a1=1.5, a2=2.2857, b=77.8569를 사용해 3D 평면 그래프를 그리는 코드이다.
이 코드는 입력 데이터 대해 y 값을 계산하고, 이를 평면으로 시각화한다.
# 학습된 모델의 파라미터
a1_rst = 1.5
a2_rst = 2.2857
b_rst = 77.8569
# 3D 축 생성
ax = plt.axes(projection='3d')
# 학습된 직선(평면)의 예측 값 계산
# 3D 평면을 위한 x1, x2 좌표 생성
x1_range = np.linspace(min(x1), max(x1), 10) # x1 범위
x2_range = np.linspace(min(x2), max(x2), 10) # x2 범위
x1_grid, x2_grid = np.meshgrid(x1_range, x2_range) # 그리드를 생성
y_pred = a1_rst * x1_grid + a2_rst * x2_grid + b_rst # 예측 평면 계산
# 3D 산점도 (실제 데이터)
ax.scatter(x1, x2, y, color='blue', label='Actual Data')
# 학습된 평면 시각화
ax.plot_surface(x1_grid, x2_grid, y_pred, color='orange', alpha=0.7, label='Prediction Plane')
# 축 라벨 설정
ax.set_xlabel('study_hours(x1)')
ax.set_ylabel('private_class(x2)')
ax.set_zlabel('Score(y)')
ax.set_title('3D Linear Regression Visualization')
# 범례 추가
ax.legend()
# 그래프 표시
plt.show()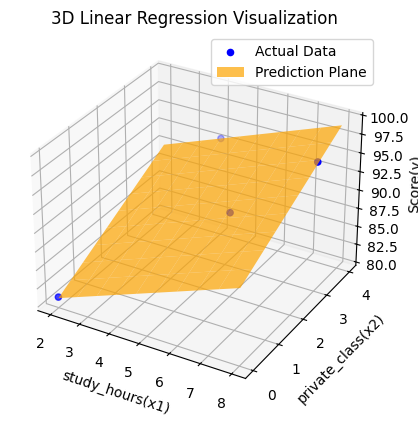
5장 참 거짓 판단 장치 : 로지스틱 회귀
딥러닝 과정에서는 전달받은 정보를 참과 거짓 중 하나로 판단해 다음 단계로 넘기는 과정이 반복된다.
이때 참과 거짓 중, 하나를 내놓는 과정을 로지스틱 회귀라고 한다.
로지스틱 회귀는 회귀라는 이름이 붙어 있지만 사실은 분류 문제를 해결하는 데 사용되는 모델이다. 쉽게 말해, 주어진 데이터를 분석해서 특정 데이터가 어느 그룹(클래스)에 속할지 예측하는 데 사용된다. 예를 들어, 이메일이 스팸인지 아닌지를 예측하거나, 환자가 병에 걸렸는지 아닌지를 판단하는 문제가 이에 해당한다.
로지스틱 회귀의 핵심은 데이터를 기반으로 특정 사건이 발생할 확률을 예측한다는 점이다. 확률값은 항상 0과 1 사이여야 하므로, 이를 보장하기 위해 시그모이드 함수라는 수학적 함수를 사용한다. 이 함수는 입력값을 0과 1 사이의 값으로 변환하는 역할을 한다.
1. 로지스틱 회귀의 정의
로지스틱 회귀를 이용해 참과 거짓을 판단하고 주어진 입력 값의 특징을 추출하는데, 이를 저장하여 모델로 사용한다.
이 모델을 이용해 비슷한 데이터의 예측 필요시에 판단 결정을 내리는데, 이 과정이 딥러닝의 동작 원리이다.
로지스틱 회귀는 좌표의 형태가 직선인 선형 회귀가 아니라 참과 거짓(혹은 성공과 실패)으로 이루어지는 이진 문제에서 용이하다.
예시로 공부한 시간에 따른 합격 여부를 표로 나타내면 다음과 같다.

이를 시그모이드 함수(형태)로 표현하면 다음과 같다.

시그모이드 함수
[모두의 딥러닝] #1. 딥러닝 시작을 위한 준비 운동
REBOOT : 기존의 블로그와는 다르게 공부하면서 새로 배우거나 중요한 내용만 작성하는 형태로 포스팅함.[1] 나의 첫 딥러닝인공지능/머신러닝/딥러닝의 차이인공지능 (Artificial Intelligence, AI)인공
udangtangtang-cording-oldcast1e.tistory.com
시그모이드 함수는 입력 값을 0과 1 사이의 값으로 변환하는 비선형 활성화 함수이다.
이 함수는 이진 분류와 같은 문제에서 주로 사용되며, 입력 값이 커질수록 출력 값은 1에 가까워지고, 작아질수록 출력 값은 0에 가까워지는 S자 형태를 가진다.
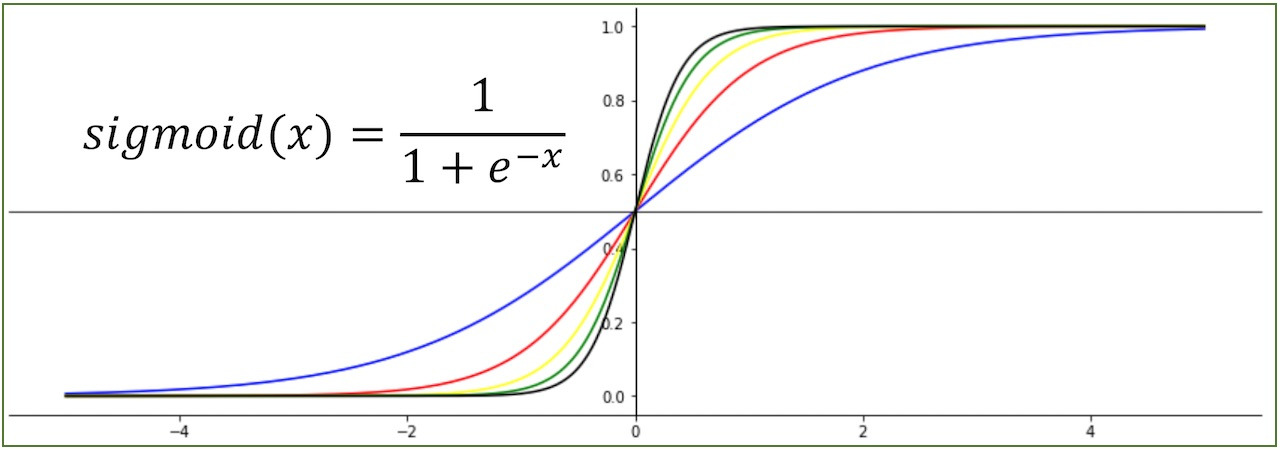
시그모이드 함수는 출력 값의 범위를 제한하기 때문에 딥러닝 모델에서 학습을 안정적으로 유지할 수 있다. 특히 출력 값이 확률로 해석되기 때문에 이진 분류 문제에서 예측 결과를 해석하기에 유리하다. 신경망의 출력층에서 주로 사용되며, 출력 값이 특정 클래스에 속할 확률로 해석될 수 있다.
2. 시그모이드 함수와 로지스틱 회귀
앞서 언급한 시그모이드 함수의 x에 ax+b가 들어갈 수 있다. 결국 우리가 구해야 하는 값도 ax+b이며 이는 선형 회귀와 비슷한 방식이다.
이때 a는 그래프의 경사도를 결정하며, b는 그래프의 좌우이동을 결정한다.
 |
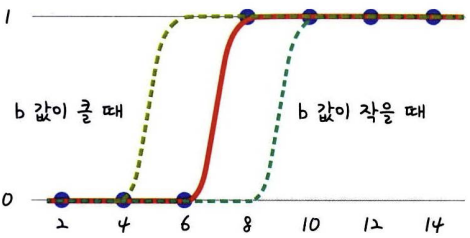 |
결국 변화하는 a와 b값에 따라 오차의 값도 아래와 같이 변화한다.
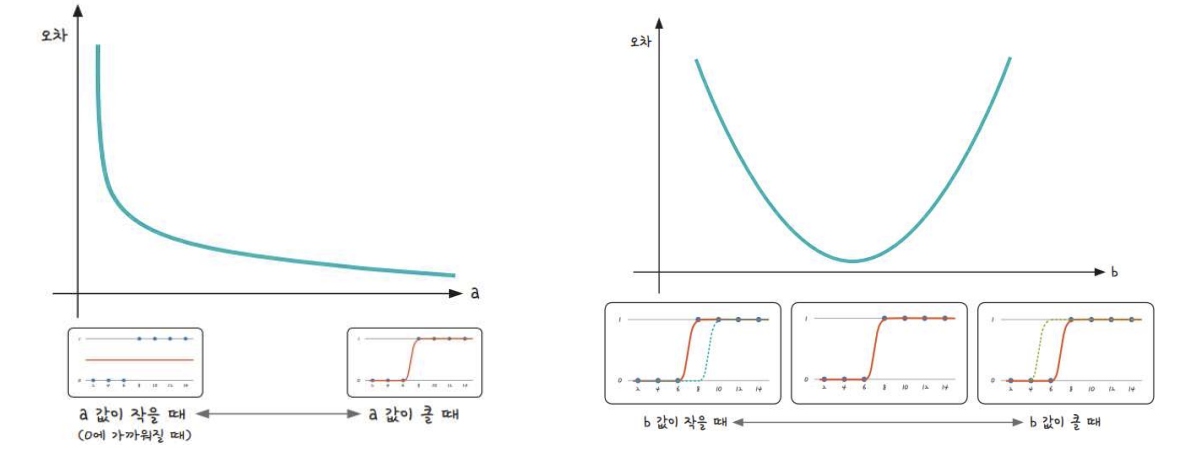
3. 오차 공식
결국 a와 b를 구하는 것은 돌고 돌아 경사하강법을 사용해야 한다. 이젠 경사하강법은 신이야...
하지만 주의해야 할 점은 시그모이드 함수는 y값이 0과 1 사이라는 점이다. 따라서 실제값이 1일 때 0에 가까워지거나 실제값이 0일 때 1에 가까워지면 오차가 증가하도록 설정해야 한다.
이 문제를 로그함수를 이용해 해결할 수 있다.
4. 로그 함수
 |
x축 : 예측값 y축 : 오차 빨간선 : 실제값이 0일때 사용할 함수 - 0으로 가까워질 수록 오차가 감소 - 1으로 가까워질수록 오차가 증가 파란선 : 실제값이 1일때 사용할 함수 - 0으로 가까워질 수록 오차가 증가 - 1으로 가까워질수록 오차가 감소 |
실제 값이 1인 경우 -log(x)를 사용하며, 0일 때는 -log(1-x)의 그래프를 사용해야 한다.
이는 아래와 같은 방법으로 해결가능하다. (x자리에 h를 대입하면 동일하다.) y에 실제 값을 대입하여 사용한다.
이를 통해 실제값에 따라 빨간색 그래프와 파란색 그래프를 적절히 선택하여 사용가능하다.

5. 코딩으로 확인하는 로지스틱 회귀
공부 시간과 합격 여부 리스트를 다음과 같이 선언한다.
data = [[2, 0], [4, 0], [6, 0], [8, 1], [10, 1], [12, 1], [14, 1]]
x_data = [i[0] for i in data] # 공 부 한 시 간 데이터
y_data = [i[1] for i in data] # 합격 여부
이를 2차원에서 표현하면 다음과 같다.
import matplotlib.pyplot as plt
plt.scatter(x_data, y_data)
plt.xlim(0, 15)
plt.ylim (-.1 , 1.1)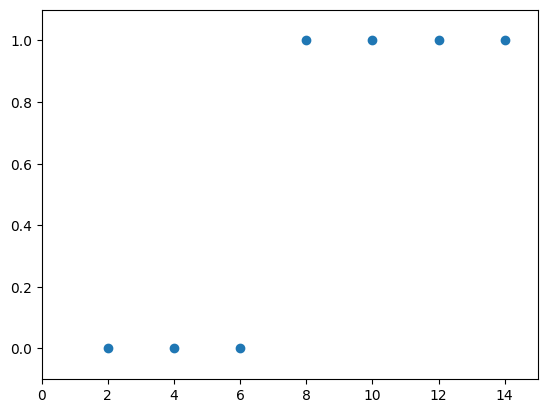
기울기 a와 절편 b의 값을 초기화하고, 학습률을 지정한다.
이후 시그모이드 식을 그대로 코드에 반영한다.
a = 0
b = 0
lr = 0.05
def sigmoid(x):
return 1 / (1+np.e ** (-x))경사하강법 적용
a와 b로 편미분 한 값에 학습률을 곱해 각각 업데이트 하는 방법은 앞선 선형회귀의 과정과 동일하나, 앞서 언급했듯 오차를 구하는 함수가 다르므로 a와 b로 편미분한 값인 a_diff와 b_diff를 결정하는 식의 변화가 생긴다. 이를 반영해 식을 수정하면 다음과 같다.
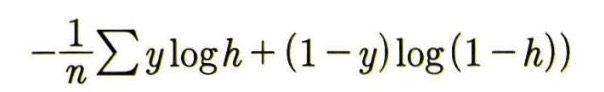
위 공식은 다음과 같이 표기된다.
J(a, b) = -(1/n) * Σ [y * log(h) + (1 - y) * log(1 - h)]
• y: 실제 값으로, 클래스 1 (참) 일 경우 1, 클래스 0 (거짓) 일 경우 0을 나타낸다.
• h: 예측 확률값으로, 시그모이드 함수에서 출력된 값이다. 이 값은 0과 1 사이의 확률을 의미한다.
• log(h): 예측 확률이 참일 때의 손실 값을 계산한다. 예측 확률이 1에 가까울수록 손실 값이 작아진다.
• log(1 - h): 예측 확률이 거짓일 때의 손실 값을 계산한다. 예측 확률이 0에 가까울수록 손실 값이 작아진다.
• n: 데이터의 개수로, 모든 데이터에 대한 평균 손실을 계산하기 위해 사용된다.
이 함수는 값이 1인 경우와 0인 경우 모두를 고려하여 모델의 전체적인 예측 오류를 계산한다.
for i in range(2001) :
for x_data, y_data in data :
a_diff = x_data*(sigmoid(a*x_data + b) - y_data)# a에 관한 편미분. 앞서 정의한 sigmoid 함수 사용
b_diff = sigmoid(a*x_data + b) - y_data# b에 관한 편미분
a = a - lr * a_diff # a를 업데이트 하기 위해 a - diff에 학습률 lr을 곱한 값을 a에서 뺌
b = b - lr * b_diff# b를 업데이트 하기 위해 b - d _ 학습률 lr을 곱한 값을 b에서 뺌
이제 위 공식을 이용해 학습을 시키기 위해 다음과 같은 코드를 실행한다.
# 1,000번 반복될 때마다 각 x_data 값에 대한 현재의 a 값, b 값 출력
for i in range(2001):
for x_data, y_data in data:
a_diff = x_data*(sigmoid(a * x_data + b) - y_data)
b_diff = sigmoid(a * x_data + b) - y_data
a = a - lr * a_diff
b = b - lr * b_diff
if i % 1000 == 0:
print("epoch = %.f, 기울기 = %.04f, 절편 =%.04f" % ( i, a, b))
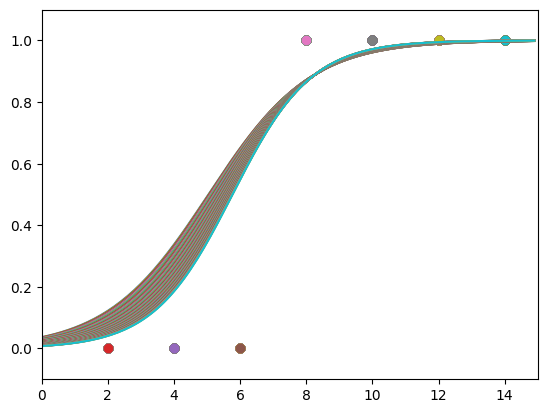
# 앞서 구한 기울기와 절편을 이용해 그래프 그리기
plt.scatter(x_data, y_data)
plt.xlim(0, 15)
plt.ylim (-.1 , 1.1)
x_range = (np.arange(0, 15, 0.1)) # 그래프로 나 타 낼 x 값의 범위 정하기
plt.plot(np.arange(0, 15, 0.1), np.array( [sigmoid(a * x + b)
for x in x_range]))
if i%100 == 0:
plt.show()
아래와 같은 학습 과정을 확인할 수 있다.
 |
 |
 |
 |
epoch = 0, 기울기 = -0.0500, 절편 =-0.0250
epoch = 0, 기울기 = -0.1388, 절편 =-0.0472
epoch = 0, 기울기 = -0.2268, 절편 =-0.0619
epoch = 0, 기울기 = 0.1201, 절편 =-0.0185
epoch = 0, 기울기 = 0.2374, 절편 =-0.0068
epoch = 0, 기울기 = 0.2705, 절편 =-0.0040
epoch = 0, 기울기 = 0.2860, 절편 =-0.0029
...
epoch = 2000, 기울기 = 1.9065, 절편 =-12.9489
epoch = 2000, 기울기 = 1.9055, 절편 =-12.9491
epoch = 2000, 기울기 = 1.8515, 절편 =-12.9581
epoch = 2000, 기울기 = 1.9057, 절편 =-12.9514
epoch = 2000, 기울기 = 1.9068, 절편 =-12.9513
epoch = 2000, 기울기 = 1.9068, 절편 =-12.9513
epoch = 2000, 기울기 = 1.9068, 절편 =-12.9513
이를 통해 시그모이드 형태의 함수의 형태로 잘 수렴하는 것을 확인할 수 있다.
하지만 아직 관문이 남아있다. 여기에서 입력 값이 추가되어 세 개 이상의 입력을 다루는 경우 소프트맥스 함수를 사용해야 한다.
이는 추후에 다루도록 한다.
6. 로지스틱 회귀에서 퍼셉트론으로
입력값을 통해 출력 값을 구하는 함수 y는 y = a1x1 + a2x2 + b로 표현되며 이를 2차원 평면 위의 직선, 초평면이라고 한다. 우리는 이 초평면을 다중 선형 회귀에서 사용했다.
우리가 아는 값 혹은 대입할 값은 독립 변수로 x1, x2이며 이를 입력값, 그리고 계산으로 얻는 y값을 출력값이라고 한다. 이를 그림으로 표현하면 아래와 같다. 바로 이 그림이 퍼셉트론의 개념이다.

퍼셉트론이란?
퍼셉트론은 딥러닝의 가장 기본적인 구성 요소로, 데이터를 보고 "참/거짓" 또는 "클래스 A/클래스 B"와 같이 이진 분류 문제를 해결하기 위한 모델이다. 퍼셉트론은 인간의 뇌가 작동하는 방식을 모방하려고 고안된 간단한 형태의 인공 신경망으로, 1958년에 프랭크 로젠블랫(Frank Rosenblatt)에 의해 개발되었다.
쉽게 말해, 퍼셉트론은 여러 입력 데이터를 받아 특정 기준에 따라 그것들을 분류하는 역할을 한다. 예를 들어, 학생의 공부 시간과 수면 시간을 입력받아 그 학생이 합격할지 여부를 예측할 수 있다.